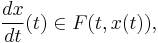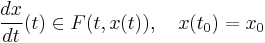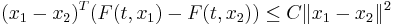Differential inclusion

In mathematics, differential inclusions are a generalization of the concept of ordinary differential equation of the form

\frac{dx}{dt}(t)\in F(t,x(t)),

where F(t, x) is a set rather than a single point in 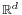\scriptstyle{\Bbb R}^d. Differential inclusions arise in many situations including differential variational inequalities, projected dynamical systems, dynamic Coulomb friction problems and fuzzy set arithmetic.

For example, the basic rule for Coulomb friction is that the friction force has magnitude μN in the direction opposite to the direction of slip, where N is the normal force and μ is a constant (the friction coefficient). However, if the slip is zero, the friction force can be any force in the correct plane with magnitude smaller than or equal to μN Thus, writing the friction force as a function of position and velocity leads to a set-valued function.

Theory

Existence theory usually assumes that F(t, x) is an upper semi-continuous function of x, measurable in t, and that F(t, x) is a closed, convex set for all t and x. Existence of solutions for the initial value problem

\frac{dx}{dt}(t)\in F(t,x(t)), \quad x(t_0)=x_0

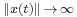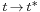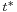for a sufficiently small time interval [t0, t0 + ε), ε > 0 then follows. Global existence can be shown provided F does not allow "blow-up" (\scriptstyle \Vert x(t)\Vert\,\to\,\infty as \scriptstyle t\,\to\, t^* for a finite \scriptstyle t^*).

Existence theory for differential inclusions with non-convex F(t, x) is an active area of research.

Uniqueness of solutions usually requires other conditions. For example, suppose 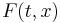F(t,x) satisfies a one-sided Lipschitz condition:

(x_1-x_2)^T(F(t,x_1)-F(t,x_2))\leq C\Vert x_1-x_2\Vert^2

for some C for all x1 and x2. Then the initial value problem

\frac{dx}{dt}(t)\in F(t,x(t)), \quad x(t_0)=x_0

has a unique solution.

This is closely related to the theory of maximal monotone operators, as developed by Minty and Haïm Brezis.

Applications

Differential inclusions can be used to understand and suitably interpret discontinuous ordinary differential equations, such as arise for Coulomb friction in mechanical systems and ideal switches in power electronics. An important contribution has been made by Filippov, who studied regularizations of discontinuous equations. Further the technique of regularization was used by Krasovskii in the theory of differential games.

References